Un matemático de la Universidad de Harvard ha dado solución a »El problema de las n-reinas» planteado en 1869.
El origen
»El problema de las n-reinas» ha supuesto un reto para muchos ajedrecistas y matemáticos durante más de 150 años. Este problema no es más que una versión ampliada de »El problema de las 8 reinas», planteado por Max Bezzel en 1848. Las primeras soluciones al problema inicial surgen en 1950 generando nuevas inquietudes en la mente de los mas curiosos. Así, el problema se hizo mucho mas complejo, tanto que no ha sido hasta este pasado año cuando Michael Simkin ha ofrecido una respuesta casi definitiva.
Breve introducción al problema
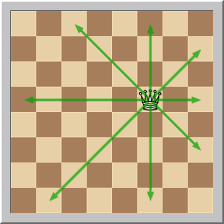
Para comprender el problema imaginaremos un tablero de ajedrez, es decir, 64 casillas organizadas en 8 filas y 8 columnas. Durante una partida de ajedrez 16 piezas a cada lado del tablero se enfrentan en una batalla estratégica. Cada pieza se mueve de una forma particular y hay una serie de normas que hacen el juego muy complejo. Sin embargo, para entender el problema nos centraremos solo en la Reina, que puede moverse tantas casillas como quiera en la dirección que quiera (horizontal, vertical y diagonal). También nos serviremos del concepto de ataque en ajedrez con ayuda de la imagen que podemos ver abajo. Una pieza se considera que está siendo atacada cuando se encuentra en cualquier casilla a dónde se pueda mover nuestra reina
El problema de las n-reinas
De acuerdo a este concepto de ataque el problema de las 8-reinas plantea lo siguiente: ¿De cuántas formas puedo colocar 8 reinas en un tablero de 8×8 sin que se ataquen entre sí?. A quién tenga un espíritu mas empírico le animo a intentarlo si dispone de un tablero de ajedrez a mano. A quién le falte el espíritu empírico o el tablero le diré que la respuesta es 92, aunque la mayoría son variantes de 12 soluciones fundamentales. Esta respuesta se encontró en 1950, plantando la semilla que florecería en 1869 en forma de una nueva pregunta. ¿De cuántas formas puedo colocar 100 reinas en un tablero de 100×100 sin que se ataquen entre sí? ¿Y en 1000 reinas en un 1000×1000?. En el mundo de las matemáticas esta situación se describe de la siguiente forma: ¿De cuántas formas puedo colocar »n» reinas en un tablero de »n» x »n» sin que se ataquen entre sí?
A calcular!
En su artículo Michael Simkin obtiene una fórmula que nos da una respuesta aproximada del problema. Pese a que es aproximada, es sin duda lo mas cerca que hemos estado de la solución desde que se planteó. Habría (0.143n)n formas posibles de colocar las reinas cumpliendo con la pacífica premisa del problema. Supongamos un tablero de 1.000.000 x 1.000.000 y 1.000.000 reinas que colocar. Multiplicamos 0.143×1.000.000 y obtenemos 143.000. Por la tanto la respuesta sería 143.0001.000.000 , un número con 5 millones de dígitos que nos casi imposible imaginar. En Microsoft Word con un tamaño de letra de 11 nos harían falta 1667 páginas sin dejar ni un solo hueco para escribir el número.
La respuesta exacta
El matemático afirma que en la teoría deberíamos poder encontrar una respuesta mas precisa pero que »personalmente, puedo terminar con el problema de las n-reinas por un tiempo». Aún así, las respuesta al problema de las n-reinas ha supuesto un avance en el ámbito de la combinatoria, una rama de las matemáticas. Simkin ha estado los últimos cinco años trabajando en la fórmula del problema, tan sumergido en el mundo del ajedrez que incluso ha soñado con este longevo juego. Ahora su idea es seguir adelante con su vida, pasando el testigo a otros matemáticos en el mundo de las n-reinas y en sus nuevas variantes.
Suficiente ajedrez por hoy!